之后博主会出一个系列专门记录CodeTop高频算法题的一个详解,一次更新20道,也就是一页的数量。更多答案也可以关注我的GitHub算法仓库——Algorithm
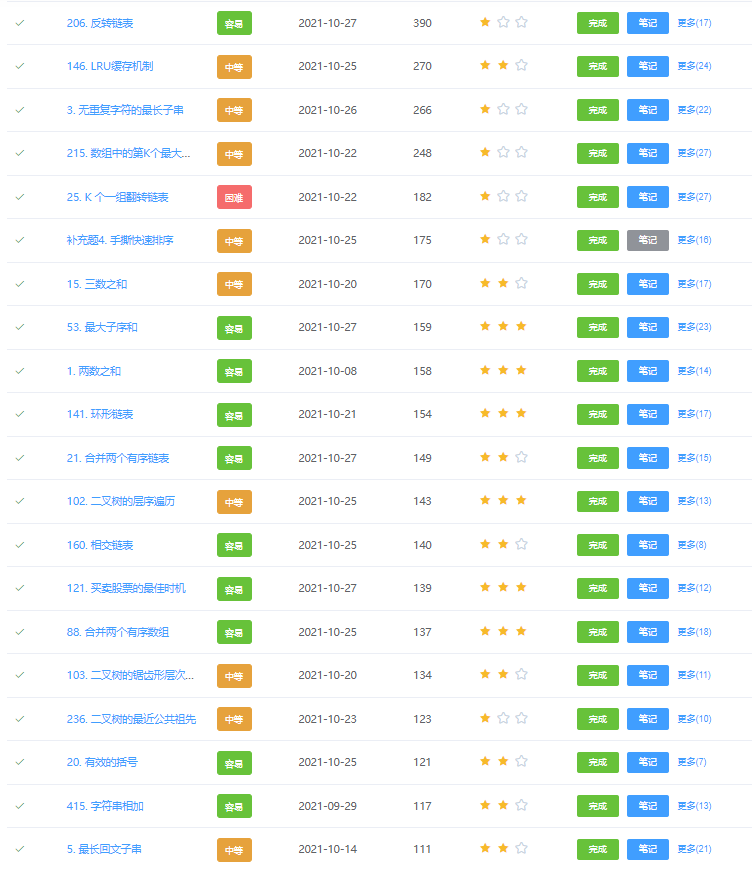
(大家可以根据我每道题打的星来衡量这道题的难易,星越少越难)
基础数据结构:
class ListNode {
int val;
ListNode next;
ListNode() {}
ListNode(int val) { this.val = val; }
ListNode(int val, ListNode next) { this.val = val; this.next = next; }
}
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {}
TreeNode(int val) { this.val = val; }
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
}206.反转链表
这应该是链表里最基础、最常问的一道算法题了,相比链表简单的插入删除要复杂一些,可以根据代码把图画一遍方便理解,但还是容易忘,记住要点是一个 while 循环里四行ListNode的交换操作:
public ListNode reverseList(ListNode head) {
ListNode prev = null, next = null;
while (head != null) {
next = head.next;
head.next = prev;
prev = head;
head = next;
}
return prev;
}146.LRU缓存机制
这道题在Java里可以通过LinkedHashMap实现,但是面试肯定不能这么说,需要使用 哈希表 + 双向链表 ,可以说又是一道大量链表的操作题,有助于锻炼对链表操作的理解:
class LRUCache {
//双向链表
class DLinkedNode {
int key;
int value;
DLinkedNode prev;
DLinkedNode next;
DLinkedNode() {}
DLinkedNode(int _key, int _value) {
key = _key;
value = _value;
}
}
private Map<Integer, DLinkedNode> cache = new HashMap<>();
private int size;
private int capacity;
private DLinkedNode head, tail;
public LRUCache(int capacity) {
this.size = 0;
this.capacity = capacity;
// 使用伪头部和伪尾部节点
head = new DLinkedNode();
tail = new DLinkedNode();
head.next = tail;
tail.prev = head;
}
public int get(int key) {
DLinkedNode node = cache.get(key);
if (node == null) {
return -1;
}
moveToHead(node);
return node.value;
}
public void put(int key, int value) {
DLinkedNode node = cache.get(key);
if (node == null) {
if (size >= capacity) {
removeTail();
size--;
}
addToHead(new DLinkedNode(key, value));
size++;
}else {
node.value = value;
moveToHead(node);
}
}
//加入头部
private void addToHead(DLinkedNode node) {
node.prev = head;
node.next = head.next;
node.next.prev = node;
head.next = node;
cache.put(node.key, node);
}
//移动到头部
private void moveToHead(DLinkedNode node) {
removeNode(node);
addToHead(node);
}
//移除尾部
private void removeTail() {
removeNode(tail.prev);
}
//删除节点,记者也要更新哈希表
private void removeNode(DLinkedNode node) {
node.prev.next = node.next;
node.next.prev = node.prev;
cache.remove(node.key);
}
}3.无重复字符的最长子串
这道题的最优解是使用滑动窗口,同时需要用到Set集合,我认为还是比较有难度的
public int lengthOfLongestSubstring(String s) {
Set<Character> occ = new HashSet<Character>();
int n = s.length();
int rk = -1, ans = 0;
for (int i = 0; i < n; i++) {
if (i != 0) {
occ.remove(s.charAt(i - 1));
}
while (rk + 1 < n && !occ.contains(s.charAt(rk + 1))) {
occ.add(s.charAt(rk + 1));
rk++;
}
ans = Math.max(ans, rk - i + 1);
}
return ans;
}215.数组中的第K个最大的数
主要考查排序,大家可以把它当作考堆排的算法题。
25.K个一组翻转链表
在第一道翻转链表的基础上难度又提升了一级,需要使用到递归(这道题我当时做了好久没做出来....)
public ListNode reverseKGroup(ListNode head, int k) {
// 如果头节点为null或者节点只有一个直接返回
if (head == null || head.next == null) {
return head;
}
//保存每一段反转的头尾指针
ListNode tail = head;
//循环k次,找到尾部
for (int i = 0; i < k; i++) {
//如果不够k个就结束了,这一段不反转直接返回头部
if (tail == null) {
return head;
}
tail = tail.next;
}
//反转后记录这一段的头部
ListNode newHead = reverse(head, tail); // [ )
//这里的head其实按这一段的顺序已经是指向尾部了
// 这里的head.next需要指向下一段的头部(就是它反转后的tail)
//每一段反转后,一开始的head最后指向尾,一开始的tail最后指向头
head.next = reverseKGroup(tail, k);
return newHead;
}
//根据头尾指针反转,每一段反转后,一开始的head最后指向尾,一开始的tail最后指向头
public ListNode reverse(ListNode head, ListNode tail) {
ListNode pre = null, next = null;
while (head != tail) {
next = head.next;
head.next = pre;
pre = head;
head = next;
}
return pre;
}补充题4. 手撕快速排序
就是考快排
15.三数之和
最优解:排序+双指针
public List<List<Integer>> threeSum(int[] nums) {
Arrays.sort(nums);
List<List<Integer>> result = new ArrayList<>();
int lastA = -9999999;
for (int i = 0; i < nums.length-2; i++) {
if (nums[i] > 0) {
return result;
}
if (nums[i] == lastA) {
continue;
}
lastA = nums[i];
int lastLeft = -9999999;
int right = nums.length;
for (int j = i+1; j < right - 1; j++) {
if (nums[j] == lastLeft) {
continue;
}
for (int k = right - 1; k > j; k--) {
if (nums[i] + nums[j] + nums[k] == 0) {
List<Integer> temp = new ArrayList<>();
temp.add(nums[i]);
temp.add(nums[j]);
temp.add(nums[k]);
result.add(temp);
right = k;
break;
}
}
lastLeft = nums[j];
}
}
return result;
}53.最大子序和
动态规划,但是空间复杂度是O(1),每次只保存当前的最优解
public int maxSubArray(int[] nums) {
int res = nums[0];
for (int i = 1; i < nums.length; i++) {
if (nums[i-1] > 0) {
nums[i]+=nums[i-1];
}
res = res > nums[i] ? res:nums[i];
}
return res;
}1.两数之和
哈希表,空间换时间,每次存这个数,找哈希表里的另一半target-nums[i]
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> map = new HashMap<>();
for (int i = 0; i < nums.length; i++) {
if (map.containsKey(target-nums[i])) {
return new int[] {i, map.get(target-nums[i])};
}
map.put(nums[i], i);
}
return null;
}141.环形链表
经典链表题:快慢指针,相遇则有环,任意一个为null则无环
public boolean hasCycle(ListNode head) {
ListNode fast = head;
while (head != null && fast != null) {
head = head.next;
fast = fast.next;
if (fast != null) {
fast = fast.next;
}else {
break;
}
if (head == fast) {
return true;
}
}
return false;
}21.合并两个有序链表
思路:递归
public ListNode mergeTwoLists(ListNode l1, ListNode l2) {
if (l1 == null) {
return l2;
}
if (l2 == null) {
return l1;
}
if (l1.val < l2.val) {
l1.next = mergeTwoLists(l1.next, l2);
return l1;
}else {
l2.next = mergeTwoLists(l2.next, l1);
return l2;
}
}102.二叉树的层序遍历
典型的队列题目
public List<List<Integer>> levelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
ArrayDeque<TreeNode> queue = new ArrayDeque<>();
queue.offer(root);
while (!queue.isEmpty()) {
List<Integer> level = new ArrayList<>();
int curLevelSize = queue.size();
for (int i = 0; i < curLevelSize; i++) {
TreeNode node = queue.poll();
level.add(node.val);
if (node.left != null) {
queue.offer(node.left);
}
if (node.right != null) {
queue.offer(node.right);
}
}
res.add(level);
}
return res;
}160.相交链表
两个指针分别移动,到末尾之后移到对方链表上继续移动,相等时返回
public ListNode getIntersectionNode(ListNode headA, ListNode headB) {
if (headA == null || headB == null) {
return null;
}
ListNode pA = headA;
ListNode pB = headB;
while(pA != pB) {
pA = pA == null ? headB : pA.next;
pB = pB == null ? headA : pB.next;
}
return pA;
}121.买卖股票的最佳时机
一次for循环,每次记录最小值,以及更新最大利润
public int maxProfit(int[] prices) {
int res = 0;
int min = Integer.MAX_VALUE;
for (int i = 0; i < prices.length; i++) {
if (min > prices[i]) {
min = prices[i];
}else {
res = Math.max(res, prices[i] - min);
}
}
return res;
}88.合并两个有序数组
根据有序和空位这两个特点,我们从nums1末尾开始比较插入
public void merge(int[] nums1, int m, int[] nums2, int n) {
int n1 = m -1;
int n2 = n -1;
while (n2 >= 0) {
if (n1 >= 0 && nums1[n1] >= nums2[n2]) {
nums1[n1+n2+1] = nums1[n1];
n1--;
}else {
nums1[n1+n2+1] = nums2[n2];
n2--;
}
}
}103.二叉树的锯齿形层次遍历
这道题我也是按自己的方法去写的,也是有些麻烦,用了队列和集合倒来倒去
public List<List<Integer>> zigzagLevelOrder(TreeNode root) {
List<List<Integer>> res = new ArrayList<>();
if (root == null) {
return res;
}
Queue<Object[]> queue = new ArrayDeque<>();
Object[] arr = new Object[2];
arr[0] = root;
arr[1] = 1;
queue.offer(arr);
int cur = 1;
List<Integer> list = new ArrayList<>();
List<Object[]> tempList = new ArrayList<>();
while (queue.size() != 0) {
Object[] temp = queue.poll();
TreeNode tn = (TreeNode)temp[0];
Integer floor = (Integer)temp[1];
if (tn != null) {
if (floor % 2 == 0) {
if (tn.right != null) {
tempList.add(new Object[]{tn.right, floor + 1});
}
if (tn.left != null) {
tempList.add(new Object[]{tn.left, floor + 1});
}
}else {
if (tn.left != null) {
tempList.add(new Object[]{tn.left, floor + 1});
}
if (tn.right != null) {
tempList.add(new Object[]{tn.right, floor + 1});
}
}
if (cur == floor) {
list.add(tn.val);
}else {
res.add(list);
list = new ArrayList<>();
list.add(tn.val);
cur = floor;
}
}
if (queue.size() == 0) {
while (tempList.size() > 0) {
queue.offer(tempList.get(tempList.size() - 1));
tempList.remove(tempList.size() - 1);
}
}
}
res.add(list);
return res;
}236.二叉树的最近公共祖先(LCA)
思路是递归,但是难点在于节点的判断:
class Solution {
private TreeNode ans;
public Solution() {
this.ans = null;
}
private boolean dfs(TreeNode root, TreeNode p, TreeNode q) {
if (root == null) return false;
boolean lson = dfs(root.left, p, q);
boolean rson = dfs(root.right, p, q);
if ((lson && rson) || ((root.val == p.val || root.val == q.val) && (lson || rson))) {
ans = root;
}
return lson || rson || (root.val == p.val || root.val == q.val);
}
public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
this.dfs(root, p, q);
return this.ans;
}
}10.有效的括号
正常的思路是用栈来做的,但是可以取巧,把括号替换为空字符串来判断:
public boolean isValid(String s) {
boolean res = false;
while (s.contains("()") || s.contains("[]") || s.contains("{}")) {
s = s.replace("()", "");
s = s.replace("[]", "");
s = s.replace("{}", "");
}
if (s.length() == 0) {
res = true;
}
return res;
}415.字符串相加
模拟加法计算:
public String addStrings(String num1, String num2) {
if (num2.length() > num1.length()) {
String temp = num1;
num1 = num2;
num2 = temp;
}
int yu = 0;
String s = "";
for (int i = 1; i <= num1.length(); i++) {
int sum = 0;
int a = Integer.valueOf(num1.charAt(num1.length() - i) + "");
if (i <= num2.length()) {
int b = Integer.valueOf(num2.charAt(num2.length() - i) + "");
sum = a+b+yu;
}else {
sum = a+yu;
}
if (sum >= 10) {
yu = 1;
s = (sum-10) + s;
}else {
yu = 0;
s = sum + s;
}
}
if (yu == 1) {
s = 1 + s;
}
return s;
}5. 最长回文子串
经典动态规划,动规思路:判断一个字符串是否回文=头尾相等+中间部分回文,dp数组代表了所有长度子串是否回文:
public String longestPalindrome(String s) {
if (s == null || s.length() == 0) {
return "";
}
int len = s.length();
String res = s.charAt(0) + "";
boolean[][] dp = new boolean[len][len];
for (int j = 0; j < len; j++) {
for (int i = 0; i <= j; i++) {
if (i == j) {
dp[i][j] = true;
}else {
dp[i][j] = ((dp[i + 1][j - 1]) || (j - i < 3)) && (s.charAt(i) == s.charAt(j));
}
if (dp[i][j] && j - i > res.length() - 1) {
res = s.substring(i, j+1);
}
}
}
return res;
}